State Machine Controller

The lowest level of RoboCar control uses a State Machine to sequence and respond to events. In this case it is a Mealy machine (there is another slightly different variety called a Moore machine, but the Computational Mechanics paradigm we are working in uses Mealy's).

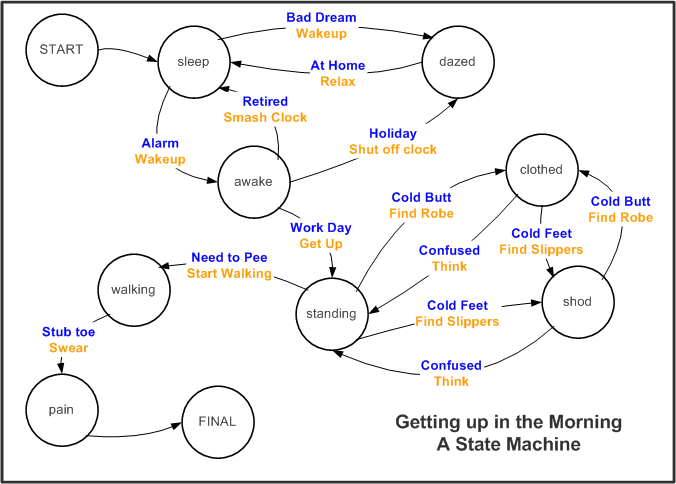
A State Machine has two basic elements and the diagrams look a little like, and have some real similarities to, network diagrams. The elements are:

• States -- the condition of the system at the time, represented as circles;
• Transitions -- a change from one State to another, shown as directional lines.

Transitions have three characteristics:

• Input -- something that happens to the system either internal or external,
                   here shown in BLUE;
• Action -- response to the input, usually a physical behavior,
                   here shown in ORANGE;
• Probability -- the likelihood that this transition will happen,
                   not shown on diagram.
  

The above picture is a cute example of sequence of events defined by a Mealy State Machine. Most machines have START and FINAL states (some run forever, so they don't have FINAL or Acceptance states), in this case we have both. The State Machine processing sequence is this:

1. We are in some State;
2. We get an Input;
3. We select and execute some Action in response to the Input;
4. We transition to another (or possibly the same) State;
5. Repeat from 2.
   

In the example we start where START indicates, in the sleep State.
There are two possible Inputs indicated: Bad Dream and Alarm.
Lets say the Alarm goes off, so we execute the Wakeup Action and transition to the awake State.
In the awake state there are three possible inputs and they are all internal realizations. Assume we know that it's a Work Day, so we decide to Get Up.
After completing the Get Up Action we are in the standing State. And the day proceeds from there (notice that the only FINAL State is pain...)

In the cases where there are multiple Input/Action transitions we can attach probabilities to each possibility. For instance in the awake State we can realize three possible Inputs: Work Day, Holiday, or Retired. We can estimate probabilities for each something like:

This makes it a Stochastic State Machine which is a fancy name for probabilistic. This is the sort of machine that the RoboCars use for their controller.